Operators in C++: Arithmetic, Relational, Logical, and More..

C++ Programming For Beginners
Operators in C++: An Overview
The operators in C++ programming act as potent instruments for data manipulation and control flow are its heart and soul. For any C++ programmer, understanding how these operators function is essential. We'll explain the main operator classifications and their importance in this condensed article. Join us in our C++ Tutorial to examine the fundamental ideas and real-world uses of operators in C++ programming.What are Operators in C++ language?
Operators are special symbols used to perform various mathematical and logical operations on variables and symbols known asoperands.
The application of operators varies depending on the context. So, it is important to understand how each type works to use them effectively when programming in C++ language.
Example
int a=10;
int b=40;
int c= a+b; Types of Operators in C++
C++ has a wide range of built-in operators that can be classified into various types according to their functionality.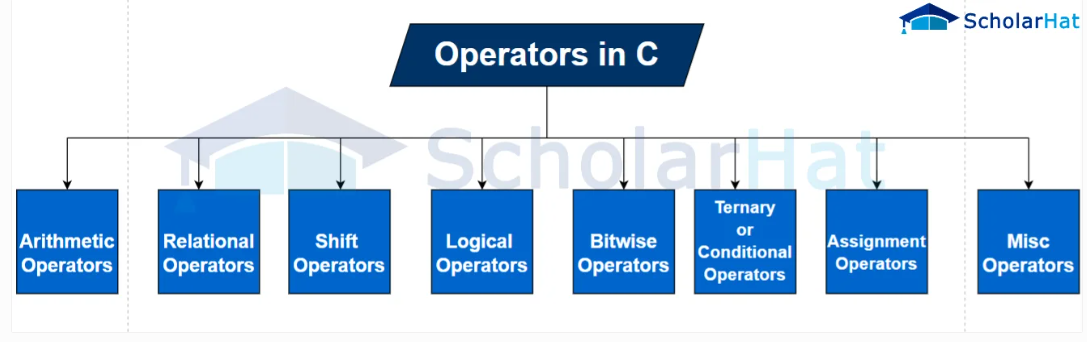
Arithmetic Operators
These operators perform basic mathematical operations like addition, subtraction, multiplication, and division. We will categorize the arithmetic operators into two categories based on the number of operands and then look at their functionality.| Type | Operator | Name of Operator | Functionality |
| Unary | ++ | Increment | Increases the value by 1 |
| - - | Decrement | Decreases the value by 1 | |
| + | Unary plus | No change in the operand value | |
| - | Unary minus | changes the negative number to the positive and vice-versa | |
| Binary | + | Addition | Add two values |
| - | Subtraction | Subtracts one value from the other | |
| * | Multiplication | Multiplies two values | |
| / | Division | Divides one by the other value | |
| % | Modulus | Finds the remainder after division |
Example to demonstrate Arithmetic Operators in C++
#include <iostream>
using namespace std;
int main() {
// Unary operators
int x = 5, y = 6, z = 7, w = 8;
cout << ++x << endl; // Increments the value of x
cout << --y << endl; // Decrements the value of y
cout << +z << endl; // Unary +
cout << -w << endl; // Unary - on a positive number
cout << -(-w) << endl; // Unary - on a negative number
// Binary operators
int a = 10, b = 3;
int sum = a + b;
int difference = a - b;
int product = a * b;
int quotient = a / b;
int remainder = a % b;
cout << "Sum: " << sum << endl;
cout << "Difference: " << difference << endl;
cout << "Product: " << product << endl;
cout << "Quotient: " << quotient << endl;
cout << "Remainder: " << remainder << endl;
return 0;
}
In the above code in C++ Compiler, we have performed all the arithmetic operations on unary as well as binary operands.
Output
6
5
7
-8
8
Sum: 13
Difference: 7
Product: 30
Quotient: 3
Remainder: 1
Read More - C++ Interview Interview Questions for Experienced
Relational Operators
They are also known as Comparison Operators. They compare the values of the two operands. The result of the comparison is either true or false. If the comparison is true, it returns 1; If the comparison results in false, it returns 0. These are known as boolean values.| Operator | Name |
| == | Equal to |
| > | Greater than |
| < | Less than |
| >= | Greater than or equal to |
| <= | Less than or equal to |
| != | Not equal to |
Example to demonstrate relational operators in C++
#include <iostream>
using namespace std;
int main() {
int x = 5;
int y = 3;
cout << (x == y) << endl; // returns 0 (false) because 5 is not equal to 3
cout << (x != y) << endl; // returns 1 (true) because 5 is not equal to 3
cout << (x > y) << endl; // returns 1 (true) because 5 is greater than 3
cout << (x < y) << endl; // returns 0 (false) because 5 is not less than 3
cout << (x >= y) << endl; // returns 1 (true) because 5 is greater than or equal to 3
cout << (x <= y) << endl; // returns 0 (false) because 5 is not less than or equal to 3
return 0;
} The above code performs all the comparison operations and returns the result in boolean values.
Output
0
1
1
0
1
0 Logical Operators
They are used to combine two or more conditions/constraints. It returns either 0 or 1 depending upon whether the expression results in true or false. If the result is true, it returns 1 else returns 0.The logical operators are used in decision-making and looping statements.
We will categorize the logical operators into two categories based on the number of operands and then look at their functionality.
| Type | Operator | Name | Functionality |
| Binary | && | Logical AND | returns 1(true) if both the expressions/values are true. |
| || | Logical OR | returns 1(true) if one of the expressions/values evaluates to true. | |
| Unary | != | Logical NOT | Negates the expression and returns 1 or 0. |
Example to demonstrate logical operators in C++ Online Compiler
#include <iostream>
using namespace std;
int main() {
int a = 1, b = 0;
if (a && b) {
cout << "Both a and b are true (non-zero)" << endl;
} else {
cout << "At least one of a or b is false (zero)" << endl;
}
if (a || b) {
cout << "At least one of a or b is true (non-zero)" << endl;
} else {
cout << "Both a and b are false (zero)" << endl;
}
if (!b) { // value of b becomes 1
cout << "b is false (zero)" << endl;
} else {
cout << "b is true (non-zero)" << endl;
}
return 0;
} The above code performs all three logical operations on a and b i.e. 1 and 0 respectively.
Output
At least one of a or b is false (zero)
At least one of a or b is true (non-zero)
b is false (zero)
Bitwise Operators
These operators work on individual bits. The operands are first converted into bits i.e. 0 or 1, and then the calculation is performed on them.We will categorize the bitwise operators into two categories based on the number of operands and then look at their functionality.
| Type | Operator | Name |
| Unary | ~ | One's complement or Bitwise Complement |
| << | Left Shift | |
| >> | Right Shift | |
| Binary | & | Bitwise AND |
| | | Bitwise OR | |
| ^ | Bitwise Exclusive OR or XOR |
Assignment Operators
These are used to assign values to the variables. The most fundamental assignment operator is=.
Example to demonstrate assignment operators in C++
#include <iostream>
using namespace std;
int main() {
int x;
x = 10; // Assigning the value 10 to x
cout << "The value of x is: " << x << endl;
return 0;
}
Output
The value of x is: 10
The following table shows some variants of the assignment operator, “=”.
| Operator | Example | Same as |
| = | x=y | x=y |
| += | x+=y | x=x+y |
| -= | x-=y | x=x-y |
| *= | x*=y | x=x*y |
| /= | x/=y | x=x/y |
| %= | x%=y | x=x%y |
| &= | x&=y | x=x&y |
| |= | x|=y | x=x|y |
| ^= | x^=y | x=x^y |
| >>= | x>>=y | x=x>>y |
| <<= | x<<=y | x=x<<y |
Conditional Operator
This is also called a ternary operator. It works on three operands. The ternary operator is used to execute a set of statements when the test expression is true and another set of statements when the test expression evaluates to false.Syntax
testexpression? expression1 : expression 2;
testexpression results in a boolean value i.e. 0(true) or 1(false).
If the testexpression evaluates to:- True: expression1 before the colon
(:)executes - False: expression2 after the colon
(:)executes
Example to demonstrate conditional operator in C++ Online Editor
#include <iostream>
using namespace std;
int main() {
int a = 5;
int b = 10;
int max = (a > b) ? a : b;
cout << "The maximum value is: " << max << endl;
return 0;
}
Output
The maximum value is: 10
Miscellaneous Operators
| Operator | Description | Example |
| returns the size of the data type | sizeof(int); // 4 |
| represents the memory address of the operand | &a; // address of a |
| accesses members of struct variables or class objects | obj.print(); |
| used with pointers to access the class or struct variables | ptr->marks = 70; |
| prints the output value | cout << 7; |
| gets the input value | cin >> a; |
Precedence of Operators in C++
Operator precedence and associativity help us to determine which operators will be given priority when there are multiple operators in the expression. It is the grouping of terms in an expression and decides how an expression should be evaluated.| Category | Operator | Associativity |
| Postfix | () [] ->. ++ - - | Left to right |
| Unary | + - ! ~ ++ - - (type)* & sizeof | Right to left |
| Multiplicative | * / % | Left to right |
| Additive | + - | Left to right |
| Shift | << >> | Left to right |
| Relational | < <= > >= | Left to right |
| Equality | == != | Left to right |
| Bitwise AND | & | Left to right |
| Bitwise XOR | ^ | Left to right |
| Bitwise OR | | | Left to right |
| Logical AND | && | Left to right |
| Logical OR | || | Left to right |
| Conditional | ?: | Right to left |
| Assignment | = += -= *= /= %=>>= <<= &= ^= |= | Right to left |
| Comma | , | Left to right |






